Gilbert-Johnson-Keerthi 2D Collision Detection
I’ve been trying to learn how collision detection works; this lead me to the Gilbert-Johnson-Keerthi (GJK) algorithm. All code samples in this post are in TypeScript. The code samples make use of some structures I have created and won’t detail in this post, but they are simple and you can see them in the GitHub repo:
VectorIShapeCollision
All the code this post uses is in a GitHub repo here: https://github.com/jthomperoo/gjk-ts-implementation This post is written based on this article and the video it recommends:
Intro
GJK is an algorithm designed to determine if two convex shapes are intersecting. It is fast, and is implemented using a generic ‘support function’ which allows for a more general approach - you can treat polygons and curved shapes such as ellipses in the same way.
Background
Minkowski Sum
GJK uses a concept called the Minkowski Sum. The Minkowski Sum is calculated by adding all the points of two shapes. For example take the two shapes below:
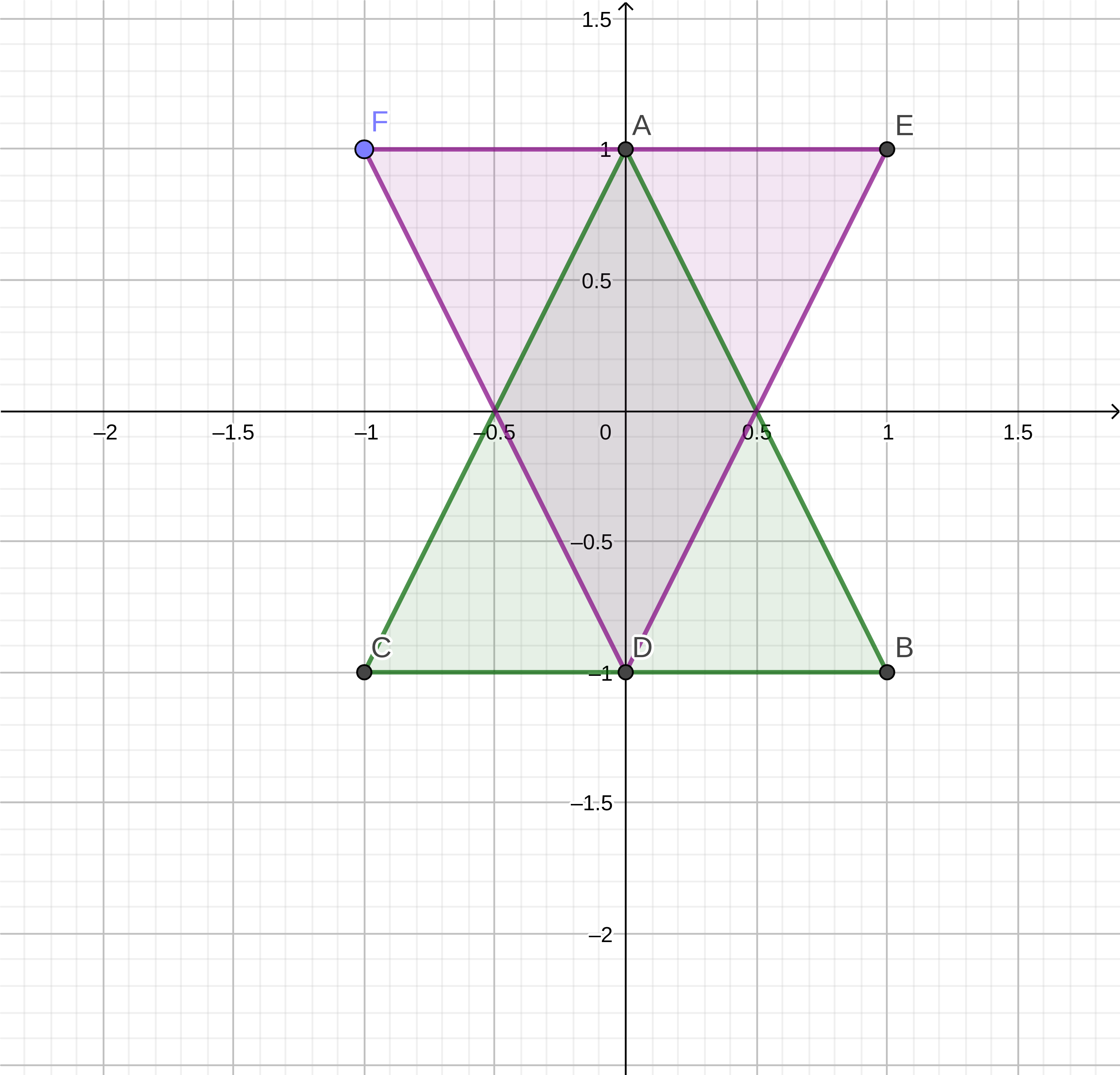
Shape A (green):
| A | B | C |
|---|---|---|
| (0,1) | (1,-1) | (-1,-1) |
Shape B (purple):
| D | E | F |
|---|---|---|
| (0,-1) | (1,1) | (-1,1) |
Taking the values of shape A and shape B we can calculate the Minkowski sum:
A + D = (0,1) + (0,-1) = (0,0) A + E = (0,1) + (1,1) = (1,2) A + F = (0,1) + (-1,1) = (-1,2) B + D = (1,-1) + (0,-1) = (1,-2) B + E = (1,-1) + (1,1) = (2,0) B + F = (1,-1) + (-1,1) = (0,0) C + D = (-1,-1) + (0,-1) = (-1,-2) C + E = (-1,-1) + (1,1) = (0,0) C + F = (-1,-1) + (-1,1) = (-2,0)
If we take these values we can plot them on a graph and see the shape it results in.
Minkowski Sum of Shape A and B: Note AD in the table and chart refers to A + D
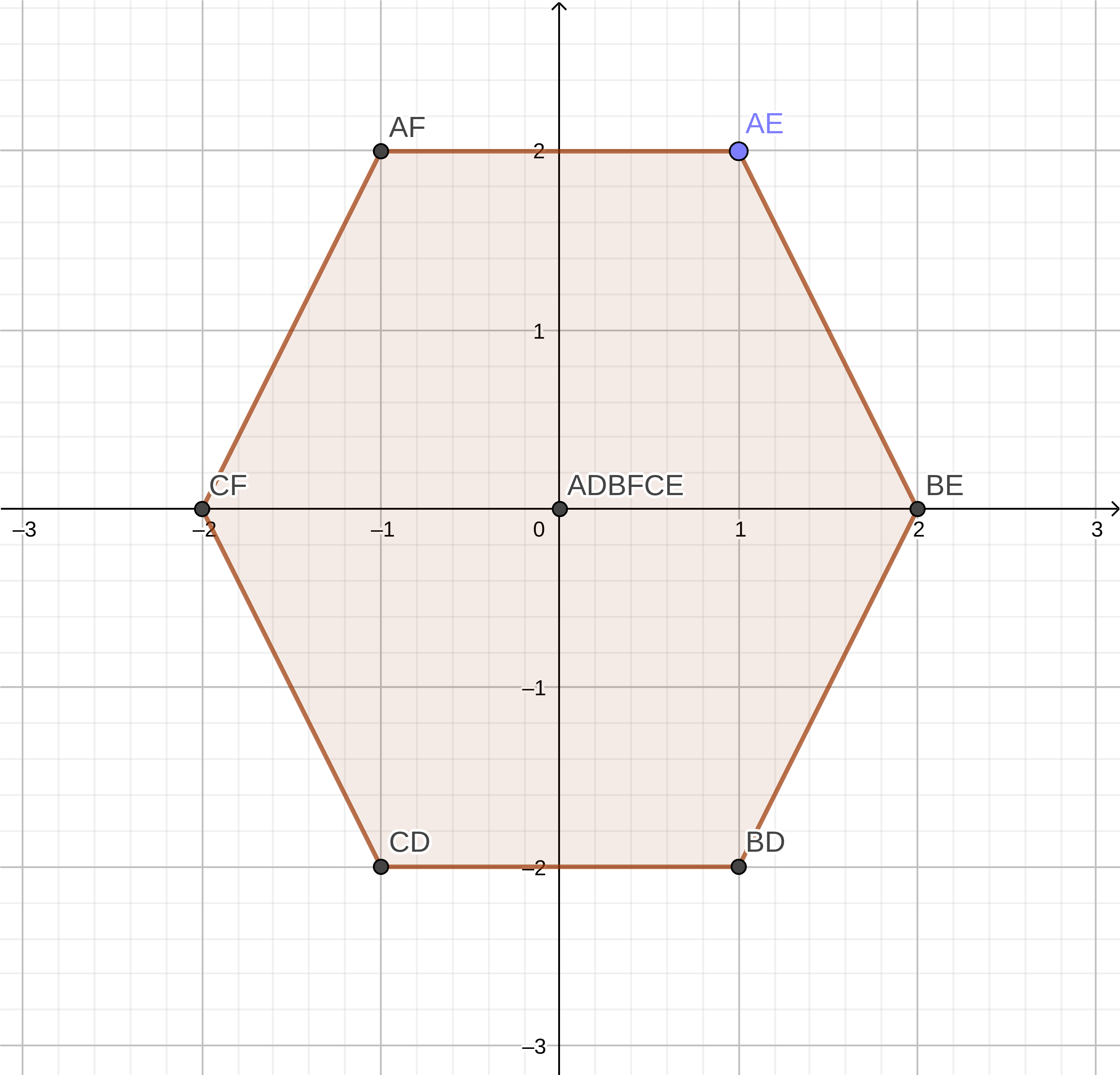
| AD | AE | AF | BD | BE | BF | CD | CE | CF |
|---|---|---|---|---|---|---|---|---|
| (0,0) | (1,2) | (-1,2) | (1,-2) | (2,0) | (0,0) | (-1,-2) | (0,0) | (-2,0) |
A nice way to think about the Minkowski Sum is imagine you take Shape A and trace the outline of Shape B with it, the shape it would result in would be the Minkowski Sum.
Minkowski Difference
GJK utilises a form of the Minkowski Sum that instead of A + B, it’s A - B. This is referred to in resources I’ve seen as the ‘Minkowski Difference’. The Minkowski Difference has the interesting property that if the two shapes are intersecting/overlapping the resulting Minkowski Difference will contain the origin. This is the basis of the GJK algorithm.
Taking the values of shape A and shape B we can calculate the Minkowski Difference:
A - D = (0,1) - (0,-1) = (0,2) A - E = (0,1) - (1,1) = (-1,0) A - F = (0,1) - (-1,1) = (1,0) B - D = (1,-1) - (0,-1) = (-1,0) B - E = (1,-1) - (1,1) = (0,-2) B - F = (1,-1) - (-1,1) = (2,-2) C - D = (-1,-1) - (0,-1) = (-1,0) C - E = (-1,-1) - (1,1) = (-2,-2) C - F = (-1,-1) - (-1,1) = (0,-2)
If we take these values we can plot them on a graph and see the shape it results in.
Minkowski Difference of Shape A and B: Note AD in the table and chart refers to A - D
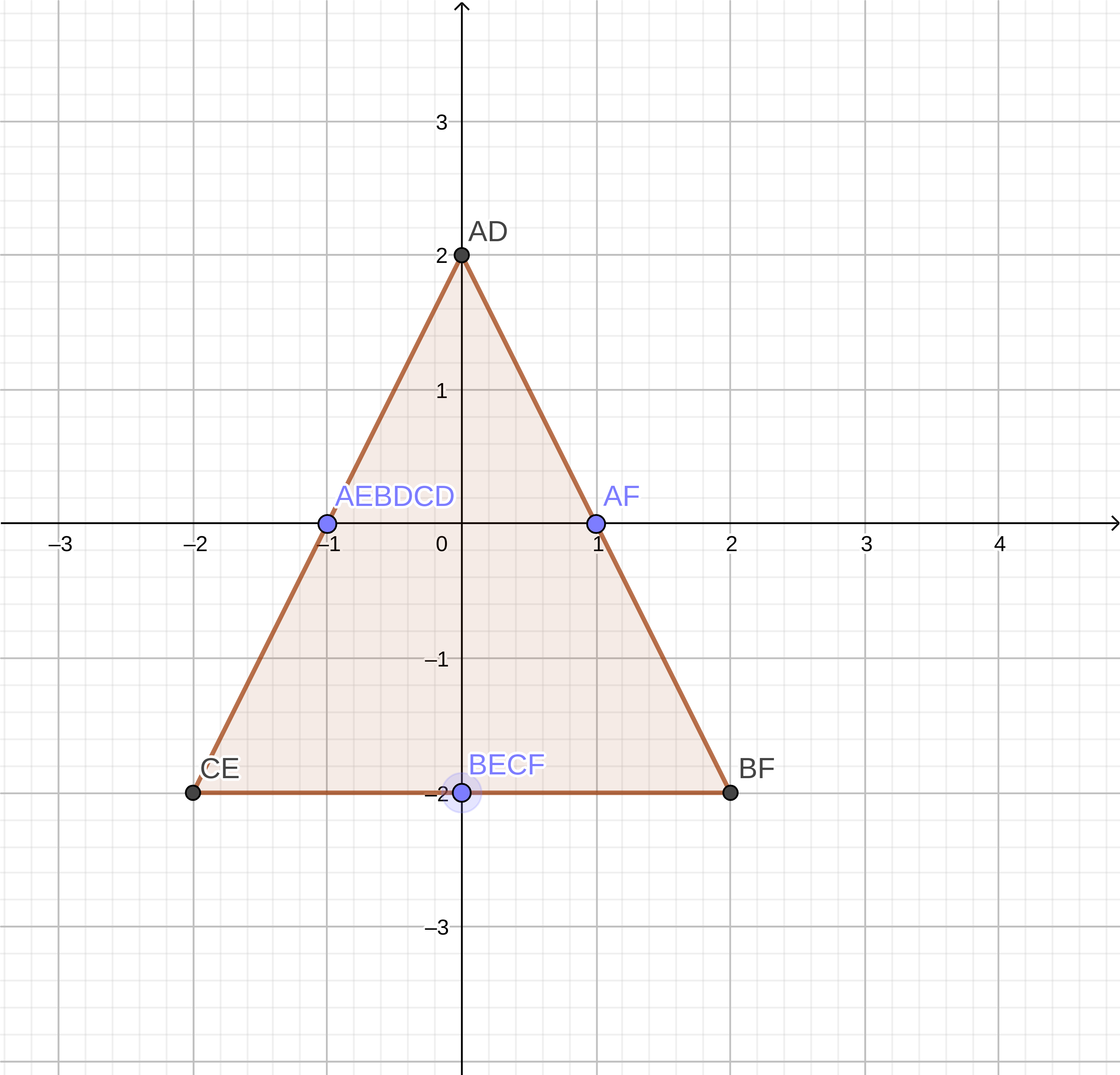
| AD | AE | AF | BD | BE | BF | CD | CE | CF |
|---|---|---|---|---|---|---|---|---|
| (0,2) | (-1,0) | (1,0) | (-1,0) | (0,-2) | (2,-2) | (-1,0) | (-2,-2) | (0,-2) |
The Algorithm
Taking these concepts the GJK algorithm optimises them. Calculating Minkowski Differences could take a long time, especially if you are checking if two shapes with many points are intersecting. In order to avoid this GJK uses two key concepts; support functions and simplexes.
Support Functions
The support function is a way to sample a point on the edge of the Minkowski Difference - without building the entire shape. The support function takes the two shapes being compared, and the direction you want to check in. The support function then takes a point from each shape, the farthest in two opposite directions. Using these two farthest points a support point can be calculated on the Minkowski Difference shape. The reason we take points from opposite directions is so that we get a point on the Minkowski Difference that will result in the largest area, so there’s a better chance we can encapsulate the origin. Since the Minkowski Difference is shape a farthest point - shape b farthest point having the point of shape b being sampled from the opposite direction results in a support point that is as far as possible in the direction provided.
The implementation of the support function is quite simple:
function support(a: IShape, b: IShape, direction: Vector): Vector {
const aFar = a.FarthestPointInDirection(direction);
const bFar = b.FarthestPointInDirection(direction.Invert());
return aFar.Sub(bFar);
}
Part of the benefit of GJK is the FarthestPointInDirection can be abstracted out and applied to Polygons and Curves. Here’s an implementation of FarthestPointInDirection for a Polygon.
class Polygon implements IShape {
public points: Vector[];
...
public FarthestPointInDirection(direction: Vector): Vector {
let farthestDistance = -Infinity;
// If there are no points, just return point 0,0
let farthestPoint: Vector = new Vector(0,0);
for (const point of this.points) {
const distanceInDirection = point.Dot(direction);
if (distanceInDirection > farthestDistance) {
farthestPoint = point;
farthestDistance = distanceInDirection;
}
}
return farthestPoint;
}
}
If you want to see how other shapes would be implemented, check out the Git repo for this post which includes a Circle representation.
Here is how the support point in direction (1,0) would be calculated for shape A and B:
- Get the farthest point for shape A; this ends up being point B (1,-1). (This can be calculated as the algorithm above does or just intuitively by looking at the chart).
- Get the farthest point for shape B; this ends up being point F (-1, 1).
- Calculate B - F; this ends up being point BF (2,-2) - this is the support point.
Simplexes
The simplex is a sample of points along the Minkowski Difference shape. Simplexes can contain up to three points. GJK uses them to try to build a triangle around the origin to determine if a collision occurs.
Building simplexes
Simplexes are built iteratively by adding support points in different directions. Each support point should be pointed in a new direction to try to build the simplex containing the origin as fast as possible. The complexity comes from deciding which direction to get the support point in next.
Determining Collision and Deciding Direction
The core algorithm is simply building up a simplex using the support function to try to encapsulate the origin. We can tell if there is no collision/intersection by checking if the support point calculated reaches the origin, if it doesn’t, the origin must be outside of the Minkowski Difference and we can say there is no collision/intersection.
function Calculate(a: IShape, b: IShape): Collision | undefined {
// Build a new Simplex for determining if a collision has occurred
const simplex = new Simplex();
// Choose an arbitrary starting direction
let direction: Vector | undefined = new Vector(0,1);
// Get the first support point and add it to the simplex
const initSupportPoint = support(a, b, direction);
simplex.Add(initSupportPoint);
// Flip the direction for the next support point
direction = direction.Invert();
// Keep iterating until the direction is undefined, this will occur when
// 'CalculateDirection' doesn't return a direction, indicating that an
// intersection has been detected
while(direction) {
const supportPoint = support(a, b, direction);
// If the support point did not reach as far as the origin,
// the simplex must not contain the origin and therefore there is no
// intersection
if (supportPoint.Dot(direction!) <= 0) {
// No intersection
return;
}
// Add the simplex and determine a new direction
simplex.Add(supportPoint);
direction = simplex.CalculateDirection();
}
// No direction calculated, intersection detected
return new Collision(a, b);
}
The complexity and guts of the algorithm are in simplex.CalculateDirection. The function determines if the origin is within the current simplex - if so it will return undefined - otherwise it will return a new direction to get a support point in to add to the simplex.
class Simplex {
private points: Vector[];
...
CalculateDirection(): Vector | undefined {
// Get a, the last point added to the simplex
const a = this.points[this.points.length - 1];
// Since a was just added, we know that the inverse of a points
// towards the origin
const ao = a.Invert();
// If the simplex is a triangle
if (this.points.length == 3) {
// B is the penultimate in the simplex
// C is the oldest point in the simplex
const b = this.points[1];
const c = this.points[0];
// Determine a->b and a->c lines
const ab = b.Sub(a);
const ac = c.Sub(a);
// Determine perpendicular of the a->b line
let abPerp = new Vector(ab.y, -ab.x);
// Check the handedness of the perpendicular, it should
// face AWAY from the simplex
if (abPerp.Dot(c) >= 0) {
abPerp = abPerp.Invert();
}
// If the origin lies outside of the simplex remove the
// point and determine a new direction in the direction
// of the perpendicular; aiming to try to encapsulate
// the origin that lies outside
if (abPerp.Dot(ao) > 0) {
this.points.splice(0, 1);
return abPerp;
}
// Determine perpendicular of the a->c line
let acPerp = new Vector(ac.y, -ac.x);
// Check the handedness of the perpendicular, it should
// face AWAY from the simplex
if (acPerp.Dot(b) >= 0) {
acPerp = acPerp.Invert();
}
// If the origin lies outside of the simplex remove the
// point and determine a new direction in the direction
// of the perpendicular; aiming to try to encapsulate
// the origin that lies outside
if (acPerp.Dot(ao) > 0) {
this.points.splice(1, 1);
return acPerp;
}
return undefined;
}
// Otherwise the simplex is just a line
// B is the penultimate point in the simplex,
// in this case the other end of the line
const b = this.points[0];
// Determine a -> b line
const ab = b.Sub(a);
// Get the perpendicular of the a->b line
let abPerp = new Vector(ab.y, -ab.x);
// Check the handedness of the perpendicular, it should
// face TOWARDS the origin
if (abPerp.Dot(ao) <= 0) {
abPerp = abPerp.Invert();
}
return abPerp;
}
}
You might wonder why we don’t check the BC line - this is because we can implicitly rule out the origin being along its perpendicular. Since the points B and C are already in the simplex, and weren’t just added in, we know that they have already been checked by a previous iteration. This could be either as part of a triangle in the simplex previously, or as a line as the first two points in the simplex - it doesn’t matter. So we can safely skip checking the BC line.
Walkthrough
This is a lot of code - and it can look confusing. Below I’ll walk through all the steps of the algorithm for Shape A and B above.
Shape A and B points:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| (0,1) | (1,-2) | (-1,-1) | (0,-1) | (1,1) | (-1,1) |
- Set up the algorithm, our inital direction is
(0,1).// Build a new Simplex for determining if a collision has occurred const simplex = new Simplex(); // Choose an arbitrary starting direction let direction: Vector | undefined = new Vector(0,1); - Get the first support point.
// Get the first support point and add it to the simplex const initSupportPoint = support(a, b, direction); simplex.Add(initSupportPoint); // Flip the direction for the next support point direction = direction.Invert();Get the farthest point of A in direction
(0,1)and B in direction(0,-1). aFar:(0,1)and bFar:(0,-1)Use these values to work out the support point. Support: aFar-bFar =(0,2)function support(a: IShape, b: IShape, direction: Vector): Vector { const aFar = a.FarthestPointInDirection(direction); const bFar = b.FarthestPointInDirection(direction.Invert()); return aFar.Sub(bFar); } - Flip the direction for the next support point and begin iterating, calculating a new support point.
Support:
(0,-3)// Flip the direction for the next support point direction = direction.Invert(); // Keep iterating until the direction is undefined, this will occur when // 'CalculateDirection' doesn't return a direction, indicating that an // intersection has been detected while(direction) { const supportPoint = support(a, b, direction); - Check if the support point reaches the origin, if not there must be no intersection. If it does reach the origin, add the point to the simplex.
In this case the support point reaches the origin.
direction:
(0,-1)Support:(0,-3)supportPoint.Dot(direction):3// If the support point did not reach as far as the origin, // the simplex must not contain the origin and therefore there is no // intersection if (supportPoint.Dot(direction!) <= 0) { // No intersection return; } // Add the simplex and determine a new direction simplex.Add(supportPoint); - At this point the Simplex is only a line, so cannot contain the origin; determine a new direction to search for the support point in.
direction = simplex.CalculateDirection();- Get the last point added to the simplex, and determine the direction to the origin, it will be the inverse of this point.
a:
(0,-3)ao:(0,3)CalculateDirection(): Vector | undefined { // Get a, the last point added to the simplex const a = this.points[this.points.length - 1]; // Since a was just added, we know that the inverse of a points // towards the origin const ao = a.Invert(); // If the simplex is a triangle if (this.points.length == 3) { - Since the Simplex is a line not a triangle, get the second point in the line and calculate the Simplex line.
b:
(0,2)ab:(0,5)// Otherwise the simplex is just a line // B is the penultimate point in the simplex, // in this case the other end of the line const b = this.points[0]; // Determine a -> b line const ab = b.Sub(a); - Calculate the perpendicular of this line and make sure it is facing towards the origin. This will be the new direction for the next support point.
abPerp:
(5, 0)abPerp.Dot(ao)0abPerp:(-5, 0)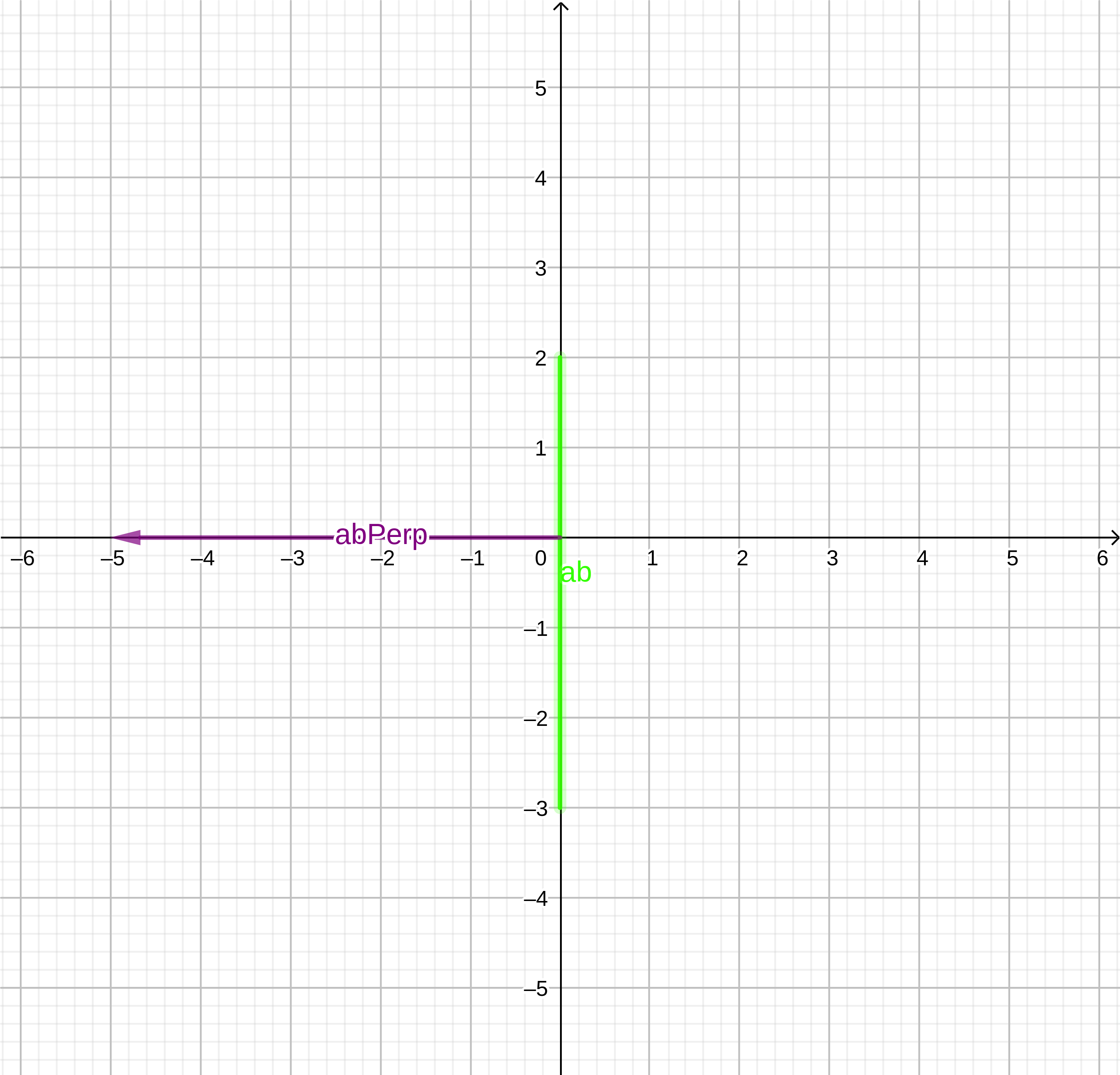
// Get the perpendicular of the a->b line let abPerp = new Vector(ab.y, -ab.x); // Check the handedness of the perpendicular, it should // face TOWARDS the origin if (abPerp.Dot(ao) <= 0) { abPerp = abPerp.Invert(); } return abPerp;
- Get the last point added to the simplex, and determine the direction to the origin, it will be the inverse of this point.
a:
- We now have a direction to search in for the next support point. We return to the start of the loop and don’t exit as we have a direction and there is no intersection found yet.
direction:
(-5, 0)Support:(-2,-2)supportPoint.Dot(direction):10Support point reached the origin, so we can’t say there is no intersection.while(direction) { const supportPoint = support(a, b, direction); // If the support point did not reach as far as the origin, // the simplex must not contain the origin and therefore there is no // intersection if (supportPoint.Dot(direction!) <= 0) { // No intersection return; } - Add the new support point to our simplex, creating a triangle. This triangle could contain the origin, if it does the simplex will return
undefinedinstead of returning a new direction to search in.// Add the simplex and determine a new direction simplex.Add(supportPoint); direction = simplex.CalculateDirection();- Get the points of the triangle simplex.
a:
(-2,-2)b:(0,-3)c:(0,2)ao:(2,2)// Get a, the last point added to the simplex const a = this.points[this.points.length - 1]; // Since a was just added, we know that the inverse of a points // towards the origin const ao = a.Invert(); // If the simplex is a triangle if (this.points.length == 3) { // B is the penultimate in the simplex // C is the oldest point in the simplex const b = this.points[1]; const c = this.points[0]; - Get ab and ac lines.
ab:
(2,-1)ac:(2,4)// Determine a->b and a->c lines const ab = b.Sub(a); const ac = c.Sub(a); - Calculate ab line perpendicular, which faces away from the simplex.
abperp:
(-1,-2)// Determine perpendicular of the a->b line let abPerp = new Vector(ab.y, -ab.x); // Check the handedness of the perpendicular, it should // face AWAY from the simplex if (abPerp.Dot(c) >= 0) { abPerp = abPerp.Invert(); } - Determine if the origin lies outside of the simplex beyond ab.
abPerp.Dot(ao):
-6Origin does not lie outside the simplex beyond ab.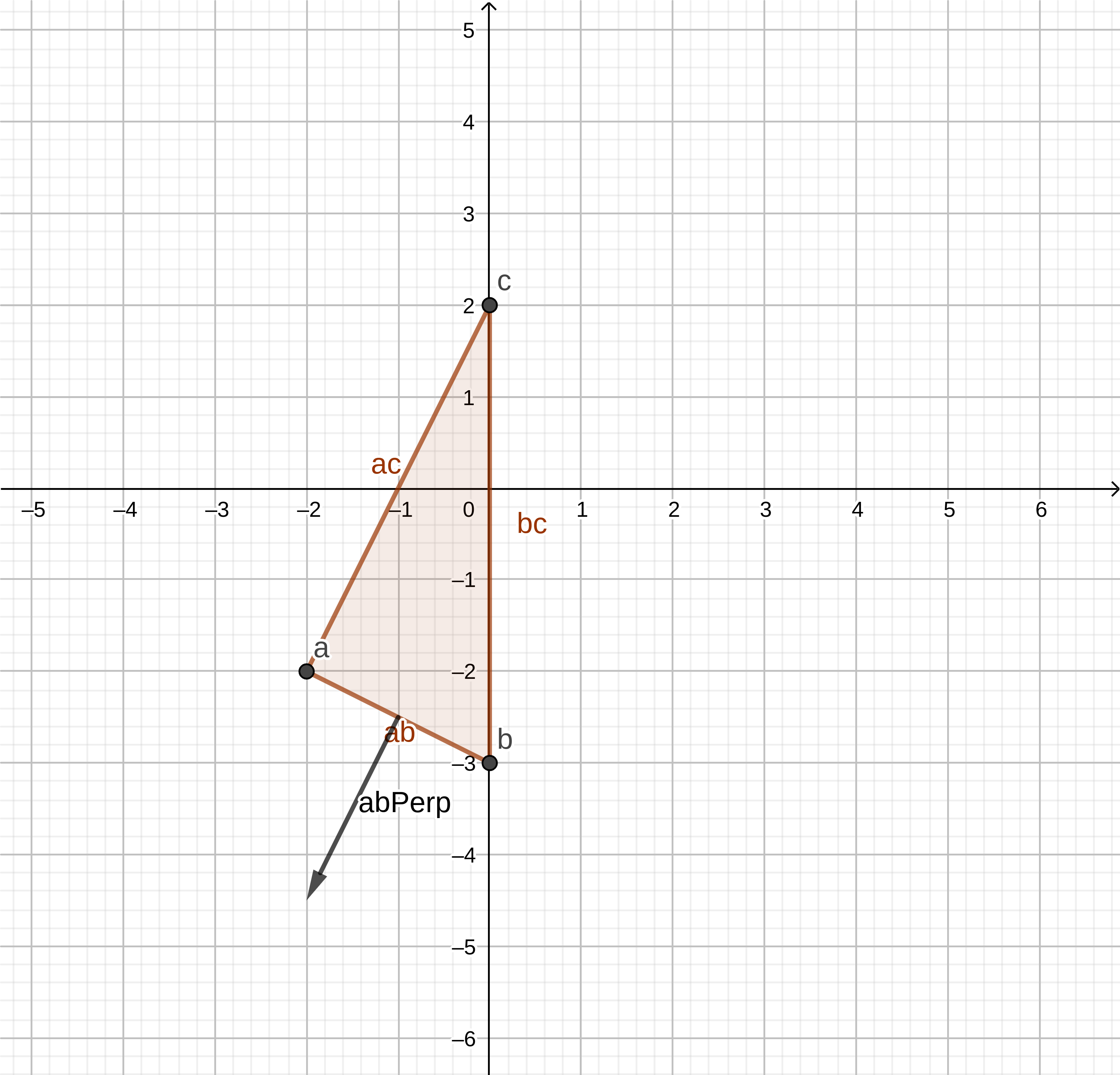
if (abPerp.Dot(ao) > 0) { this.points.splice(0, 1); return abPerp; } - Calculate ac line perpendicular, which faces away from the simplex.
acPerp:
(-4,2)// Determine perpendicular of the a->c line let acPerp = new Vector(ac.y, -ac.x); // Check the handedness of the perpendicular, it should // face AWAY from the simplex if (acPerp.Dot(b) >= 0) { acPerp = acPerp.Invert(); } - Determine if the origin lies outside of the simplex beyond ac.
acPerp.Dot(ao):
-4Origin does not lie outside the simplex beyond ab.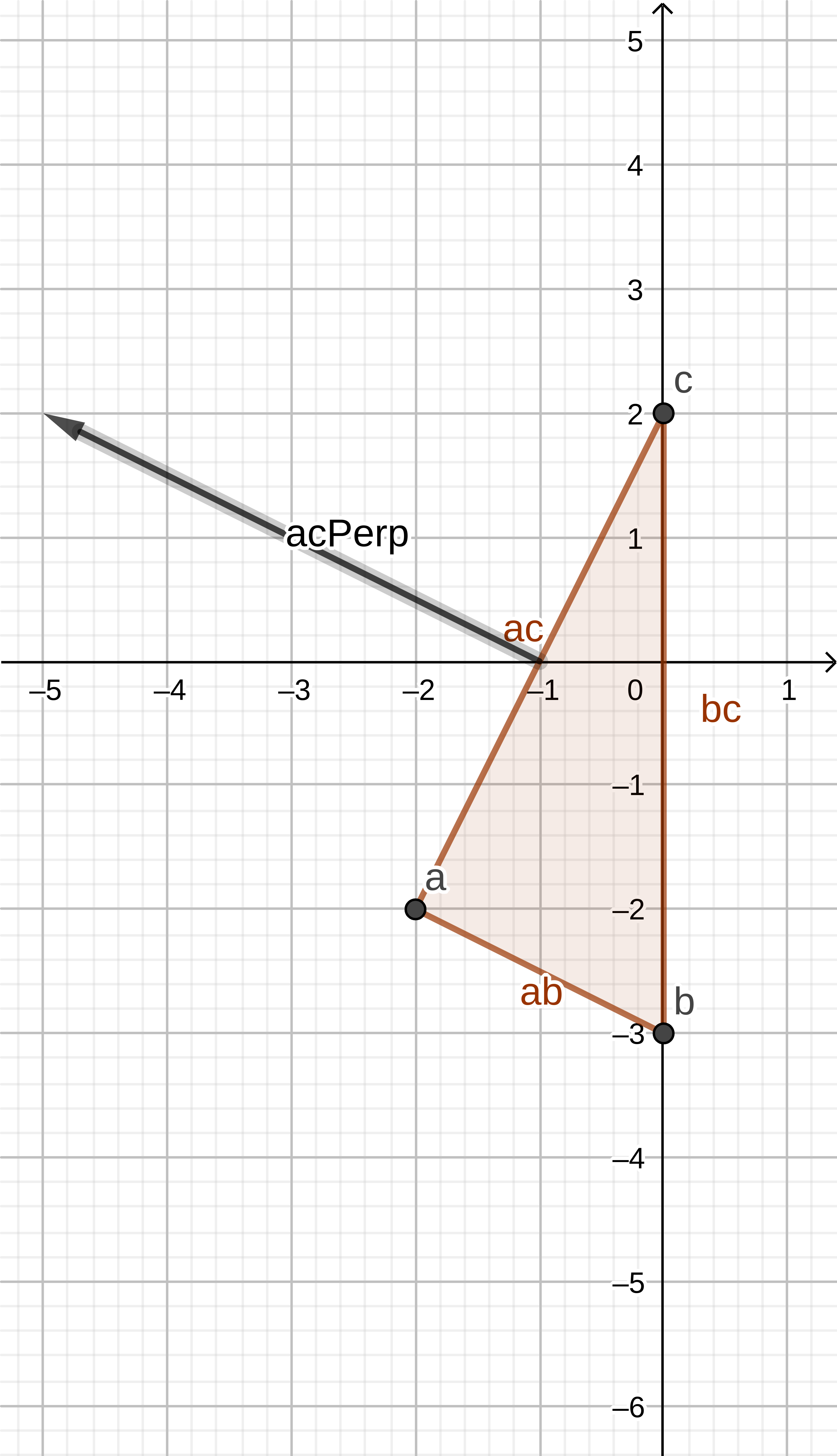
// If the origin lies outside of the simplex remove the // point and determine a new direction in the direction // of the perpendicular; aiming to try to encapsulate // the origin that lies outside if (acPerp.Dot(ao) > 0) { this.points.splice(1, 1); return acPerp; } - Since AB and AC have been checked in this iteration, and we know BC has been checked in the previous iteration, the origin must lie within the simplex, so a collision/intersection is detected - the function will return
undefinedto signal this.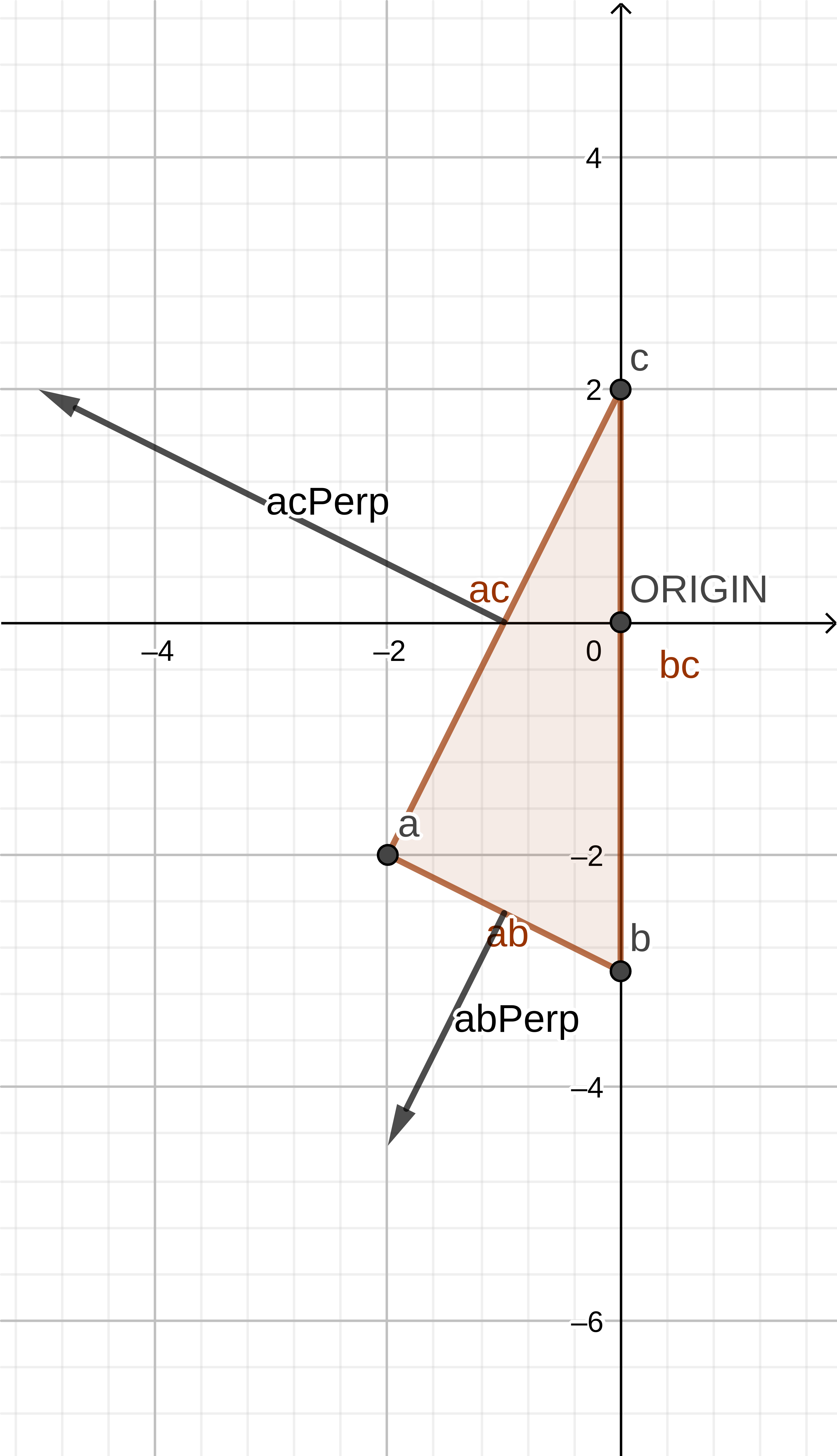
- Get the points of the triangle simplex.
a:
- Since a collision has been detected, the loop is exited and the Collision information between the two shapes is returned.
direction = simplex.CalculateDirection(); } // No direction calculated, intersection detected return new Collision(a, b);
Conclusion
Hopefully this helps you understand the GJK algorithm. The algorithm will give you a yes/no response for if two shapes are colliding. Check out the repo for this post to see a working example with polygons and circles. You are able to expand this out with additional algorithms and techniques to try to get the penetration distance between the two shapes, collision normals and contact points. The dyn4j blog has good resources on various collision detection/response algorithms; so you might want to look there for how to expand upon GJK.
